Corruptographic

TLDR: The process of breaking a flawed RSA encryption schema.

Introduction

Let's take a look at another puzzle, this one is a doozy and is infamous among my puzzles as when I released it despite running for 20 days (almost 3 weeks) and numerous clues dropped on a regular basis, it received 0 successful solves. Before we dig in let's consider why that is. 20 days isn't that long in the grand scheme since many run indefinitely, however, it should be more than sufficient to to break something as simple as this, so it's not a time limitation problem. The puzzle was released on a CyberSecurity club member puzzles page, one that is always competing in some CTF or other so it's not necessarily a lack of talent either. One could argue it didn't attract a great deal of attention with only half a dozen or so people making any sort of attempt, but this is not unusual for my puzzles and usually, they are solved fairly quickly.

I would say there are two reasons why this one is different, the first is in the specialism, this puzzle differs from my others in that it is a full encryption algorithm. Unfortunately, cryptographic experts are not that common in the industry mostly due to a dislike of maths, this club is no different it that at the time there were no clear experts in cryptography to solve it meaning this puzzle hit a weakness in the club's repertoire. Why release it then? Partly to draw attention to this weakness, so others might try to fill the gap, and partly to show that actually cryptographic maths isn't really that difficult and maybe encourage some people to try a little harder. The jury is still very much out on whether it achieved either of those aims, but the puzzle has become a bit of a focal point and acid test to work within the club on how to approach cryptography.

Before I mentioned there were two reasons, and the second is this, the nature of the puzzle is actually quite weird. Anyone who knows much about crypto will tell you the point of something being cryptographically secure rather than a cipher is that the encoded message is indiscernible from random noise, moreover immune to the kinds of attacks that ciphers were vulnerable to. So if the algorithm is truly secure the very definition should imply it's not really possible to break it, and by extension, this means that any puzzle involving breaking a cryptosystem must be using a flawed cryptosystem for complicated reasons I will go into some other time. This puzzle is no different and uses a flawed cryptosystem, what most (in fact all that I've seen) puzzles of this type focus on is that the algorithm used is subject to a known flaw such as a static seed or weak key, or even an algorithm that turned out to not be secure at all, often an outdated one. This puzzle is different, it uses a flaw of my own design, not one documented anywhere, which makes it tricky to research.

Why do that? Surely it's just impossible? Not true, this puzzle was made to teach a valuable lesson, how do you think those known flaws were found? Trial and error mostly, this puzzle was built to show the approach you would use when you can't fall back on research. It shows you what to look for, how to think rationally about breaking a cryptosystem, the significant risk in how easy it is to accidentally build a flawed cryptosystem, but above all it was built to show how difficult it is to even know when your cryptosystem is flawed, which is one of the biggest issues with new cryptosystems. This means only the really old ones can really be trusted, which leaves you in a bit of a catch-22 but that's not a problem for here, though it is worth taking away from this that it can be just as hard to know when someone has deliberately created a flaw in a cryptosystem you use. Suddenly that 0 solves starts to look a lot like a mark of success, because to all my breakers this system proved unbreakable, even though I personally told them it was flawed.

The Problem

That's enough about the mental gymnastics of why this problem proved so difficult. Let's look at the actual problem:

L34ky P1p3s

Public Key

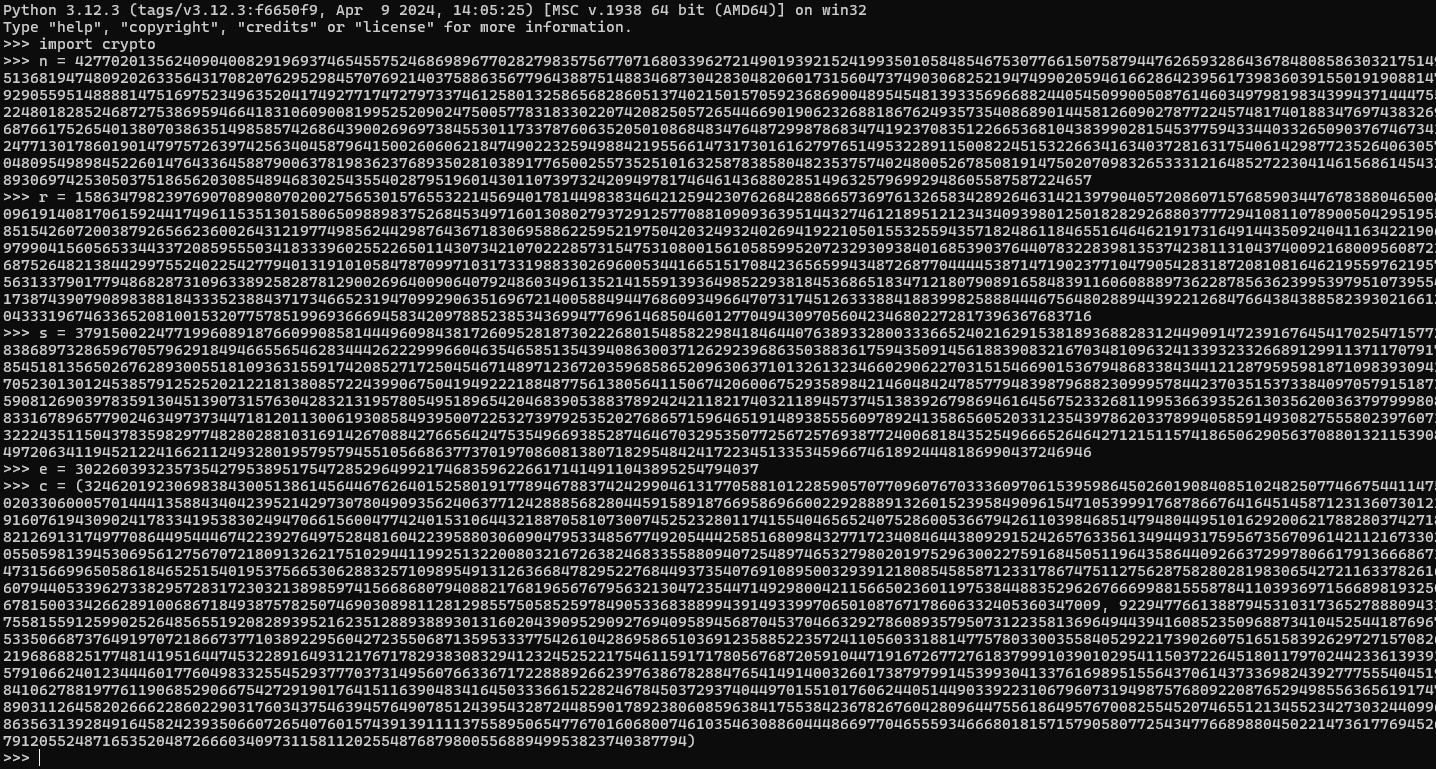
n = 427702013562409040082919693746545575246869896770282798357567707168033962721490193921524199350105848546753077661507587944762659328643678480858630321751495136819474809202633564317082076295298457076921403758863567796438875148834687304283048206017315604737490306825219474990205946166286423956173983603915501919088147929055951488881475169752349635204174927717472797337461258013258656828605137402150157059236869004895454813933569668824405450990050876146034979819834399437144475522480182852468727538695946641831060900819952520902475005778318330220742082505726544669019062326881867624935735408689014458126090278772245748174018834769743832696876617526540138070386351498585742686439002696973845530117337876063520501086848347648729987868347419237083512266536810438399028154537759433440332650903767467341247713017860190147975726397425634045879641500260606218474902232594988421955661473173016162797651495322891150082245153226634163403728163175406142987723526406305704809549898452260147643364588790063781983623768935028103891776500255735251016325878385804823537574024800526785081914750207098326533312164852722304146156861454328930697425305037518656203085489468302543554028795196014301107397324209497817464614368802851496325796992948605587587224657
r = 158634798239769070890807020027565301576553221456940178144983834642125942307626842886657369761326583428926463142139790405720860715768590344767838804650080961914081706159244174961153513015806509889837526845349716013080279372912577088109093639514432746121895121234340939801250182829268803777294108110789005042951955851542607200387926566236002643121977498562442987643671830695886225952197504203249324026941922105015532559435718248611846551646462191731649144350924041163422190697990415605653344337208595550341833396025522650114307342107022285731547531080015610585995207232930938401685390376440783228398135374238113104374009216800956087236875264821384429975524022542779401319101058478709971031733198833026960053441665151708423656599434872687704444538714719023771047905428318720810816462195597621957563133790177948682873109633892582878129002696400906407924860349613521415591393649852293818453686518347121807908916584839116060888973622878563623995397951073955417387439079089838818433352388437173466523194709929063516967214005884944768609349664707317451263338841883998258884446756480288944392212684766438438858239302166120433319674633652081001532077578519969366694583420978852385343699477696146850460127704943097056042346802272817396367683716
s = 379150022477199608918766099085814449609843817260952818730222680154858229841846440763893328003336652402162915381893688283124490914723916764541702547157728386897328659670579629184946655654628344426222999660463546585135439408630037126292396863503883617594350914561883908321670348109632413393233266891299113711707917854518135650267628930055181093631559174208527172504546714897123672035968586520963063710132613234660290622703151546690153679486833843441212879595981871098393094170523013012453857912525202122181380857224399067504194922218848775613805641150674206006752935898421460484247857794839879688230999578442370351537338409705791518735908126903978359130451390731576304283213195780549518965420468390538837892424211821740321189457374513839267986946164567523326811995366393526130356200363797999808833167896577902463497373447181201130061930858493950072253273979253520276865715964651914893855560978924135865605203312354397862033789940585914930827555802397607132224351150437835982977482802881031691426708842766564247535496693852874646703295350772567257693877240068184352549666526464271215115741865062905637088013211539084972063411945212241662112493280195795794551056686377370197086081380718295484241722345133534596674618924448186990437246946
e = 3022603932357354279538951754728529649921746835962266171414911043895254794037

Cipher Text

c = (324620192306983843005138614564467626401525801917789467883742429904613177058810122859057077096076703336097061539598645026019084085102482507746675441147502033060005701444135884340423952142973078049093562406377124288856828044591589187669586966002292888913260152395849096154710539991768786676416451458712313607301219160761943090241783341953830249470661560047742401531064432188705810730074525232801174155404656524075286005366794261103984685147948044951016292006217882803742718821269131749770864495444674223927649752848160422395880306090479533485677492054442585168098432771723408464438092915242657633561349449317595673567096142112167330205505981394530695612756707218091326217510294411992513220080321672638246833558809407254897465327980201975296300227591684505119643586440926637299780661791366686714731566996505861846525154019537566530628832571098954913126366847829522768449373540769108950032939121808545858712331786747511275628758280281983065427211633782616607944053396273382957283172303213898597415668680794088217681965676795632130472354471492980042115665023601197538448835296267666998815558784110393697156689819325067815003342662891006867184938757825074690308981128129855750585259784905336838899439149339970650108767178606332405360347009, 92294776613887945310317365278880943375581559125990252648565519208289395216235128893889301316020439095290927694095894568704537046632927860893579507312235813696494439416085235096887341045254418769675335066873764919707218667377103892295604272355068713595333775426104286958651036912358852235724110560331881477578033003558405292217390260751651583926297271570826219686882517748141951644745322891649312176717829383083294123245252217546115917178056768720591044719167267727618379991039010295411503722645180117970244233613939157910662401234446017760498332554529377703731495607663367172288892662397638678288476541491400326017387979914539930413376169895155643706143733698243927775554045198410627881977611906852906675427291901764151163904834164503336615228246784503729374044970155101760624405144903392231067960731949875768092208765294985563656191747890311264582026662286022903176034375463945764907851243954328724485901789238060859638417553842367826760428096447556186495767008255452074655121345523427303244099686356313928491645824239350660726540760157439139111137558950654776701606800746103546308860444866977046555934666801815715790580772543477668988045022147361776945267912055248716535204872666034097311581120255487687980055688949953823740387794)

Above you'll find the public key and a message encrypted with it. Below you'll find some code, we think it's in Python 3.

def gen_keys() -> ((int, int, int, int), (int, int, int, int)):
p, q = getPrime(2048), getPrime(2048)
n = p*q
r = 0
while math.gcd(r, n) != 1:
r = random.randint(2, n)
s = 0
while math.gcd(s, n) != 1 and math.gcd(p + s, n) != 1:
s = random.randint(2, n) * 2
t = math.lcm(p-1, q-1)
e = 0
while math.gcd(e, t) != 1:
e = random.randint((1<<16)+1, (1<<256)+1)
d = modInverse(e, t)
return (n, r, s, e), (p, q, t, d)

def encrypt(message: str, pubkey: (int, int, int, int), privkey: (int, int, int, int)) -> int:
n, r, s, e = pubkey
p, q, t, d = privkey
m = bytes_to_long(message.encode('utf-8'))
return modDivide(pow(s * r, e, n), p + s, n), pow(modDivide(m, s * r, n), e, n)

This is a small snippet of the code we were able to extract before losing access. Allow me to explain what's going on...

Time has passed since the previous security incidents at our little company, and Madball Investments as it was known has been swallowed up by a giant conglomerate known as ACME Incorporated. Internally though much of the company hasn't really changed they have just expanded massively in scale, and not everyone is entirely happy with the changes, especially in management. In fact, in an effort to stop some of the more volatile employees from going rogue with the massively expanding risk of insider threat, HR made some key changes to company policies. In a word, most of the workers of Madball have unionized. We work for this new union and our team has been tasked with finding a means for whistleblowers to report their findings anonymously. Neither Madball nor our new union are prepared for achieving this so we contracted in some outside help and some folks in upper management recommended we employ a chap known as James Johnson, everyone calls him JJ, and he's a whizkid so we quickly brought him on board. Almost overnight he constructed an anonymous IM client that is fully peer-to-peer encrypted allowing our staff to report directly to our regulatory bodies about violations, only after a couple of weeks rumors started to appear that the system was bugged as key whistleblowers were mysteriously let go, if true this is a travesty.

Normally we wouldn't pay any mind to these rumors but we were soon approached by another company we had never had dealings with before. They claimed to know JJ and said that he also goes by the alias Jimmy "the leak". Apparently, he is well known for placing backdoors in his encryption algorithms that he then sells on the black market. Soon after we spoke to the National Cybercrime Agency and they told us this individual was yet to be caught but they believed he had recently switched tactics, contacting high-level directors to undermine the privacy of employees.

Attacking the Beast

Alright so that's the premise so where do we start, well, why don't we take a look at the clues that were dropped and things my breakers were able to figure out? Though for the record if this "Almost overnight he constructed an anonymous IM client" ever happens to you, it's a big red flag, nobody builds a cryptosystem overnight nevermind an IM client, they must be copied from somewhere, if so, you need to see their source because they're trusting it so you need to be able to too.

Day 3 Clue

My first piece of advice for tackling these is to forget it is about cryptography, forget that there's anything weird going on, and just run through the code so you can figure out what each of the steps does on a basic level and worry about the why later, pretend its a typical maths problem, think about how you would approach it if this were on one of your math module assignments, your intent is to solve for the data, its actually not much more complex than that.

So initially nobody really seemed to know where to start. They were overwhelmed by the idea of taking on a cryptography problem, so nobody had any suggestions until I released that hint. This is a common problem when dealing with cryptography, most security experts will simply nope out believing themselves incapable, which is something we need to change but it won't be easy. Following this clue not much improved I encouraged them to look for a red flag in the algorithm. The best they came up with was suggesting 2048 is not a prime number, while true this is completely misunderstanding the context as 2048 refers to the number of bits the prime number should have making it quite large.

Day 5 Clue

It's been a couple of days, so my next piece of advice is once I've got a basic understanding of the sequence the algorithm follows, I try to understand what each step is for, this can be quite tricky as an outsider so I tend to start by running through known cryptographic algorithms looking for similarities. As people that have done similar before will probably have noticed this is clearly based off a very well known and popular algorithm, its also quite old and weak as algorithms go, meaning many of its attack vectors are well-documented, being familiar with those can be quite useful, but not here, what you're looking for here is more of a weakness in the algorithms "improvements".

Here we have another seemingly non-committal hint, but if you think about it that is a huge clue as it not only dismisses the idea of researching the answer, it points you at exactly where you need to be looking. Of course, for us, it's nothing we don't already know, just a reassertion of the fact that this is a bespoke flaw in the implementation details. This hint had a much larger impact than the first as it engaged some critical thinking leading them to look at the code with an analytical eye, by doing so they quickly realized a few simple things, that it was an asymmetric RSA algorithm with some "funk" added, that adding things to an already functional algorithm only makes sense if you're trying to break it, but most interestingly, that something was "off" about the algorithm. To the last one I responded with this:

It's quite a contrived algorithm if I'd stuck religiously to any particular standard this wouldn't work, but by twisting it in this way I can show you some of the warning signs to watch out for in new algorithms. The biggest problem in writing corrupted cryptological algorithms is they tend to be designed to prevent the very things you're trying to do with them, the second biggest problem is how resilient they are to manipulation, again because they don't want you to do that. Both of those tripped me up multiple times in writing these.

So you can see how sometimes the simplest feelings can actually be useful in detecting this sort of foul play. A true cryptanalyst uses all their senses to detect the purpose of code, if you feel a certain way about it, ask yourself "Why?".

Day 7 Clue

So once I've got an idea of how the program runs and how it compares to the algorithm it's worth going through and isolating parts that are different, because there'll be a reason for that, and it's almost always where the weakness lies. In a more pragmatic sense I tend to list out each of the variables and what I know about them, the features of a number can tell you a lot about what it's used for, primes are hard to calculate, random can be worse, but they can also often be used to disguise things by adding noise to an algorithm that otherwise may be too easy to figure out. With this in mind I'll also consider their place in the algorithm, public key variables are known, which completely eradicates any need for doubt, private ones are more mysterious, and often there's a very good reason they're kept private, lest they undermine the very foundations of the algorithm. Finally I'll also try to map out the equation of relationships in the ciphertexts, keep in the back of your mind that the calculations are all modular which adds complexity but for the most part modular arithmetic runs parallel to the maths we are used to. Once you've pieced all of that together, you can have a good think about what it would be useful to know, and look at different ways of attaching the puzzle pieces to try get the results you want.

There isn't much to this clue apart from good advice and a good approach to disassembly of the algorithm for analysis. At the time I was hopeful it would prove insightful and lead some people down a useful path. Unfortunately, this clue was met with utter silence, I suppose people don't really like being told "Do your research" but that's how it goes I guess. For my day 9 clue I did more of a Q&A session to help resolve some of the issues with my clues not really hitting the mark.

Day 9 Clue

Regarding gen_keys().

There is indeed valuable knowledge in gen_keys() but mostly its implementing RSA, knowing the steps in that should help as it will make it clear what's unusual, though part of this problem is simply understanding how RSA works, and the caveats that come with it.

With regards to macth.gcd() and coprimality.

Check those functions more carefully, they are while loops, so they'll run until they are false, in short they literally generate new numbers until one is coprime with its required coprimal partner, but also don't worry too much about things in the public key, they are known, knowing a number usually supercedes the relevance of understanding its type, but not always, the point to take away is if you have the value you can plug them into a formula and don't really need to care how they were made.

In reference to how t is calculated.

t is something quite special, you'll need to learn more about what it is and what it does, but that is actually the standard way it is generated.

In reference to the fact that encrypt() returns two values.

This is an interesting one, usually an algorithm will just return one value, but for reasons of necessity you'll find a lot of my algorithms and those in CryptoHack return multiple, there is a reason for this, and it will become important once you reach that stage as this duality can be manipulated and exploited.

On why the coprime generator loops.

An interesting though irrelevant note is I trialed and errored a lot of different approaches to generate these, and found by far the most efficient method to be literally generating them randomly repeatedly until they met the requirements, it felt baffling but I can't argue with the figures, and upon investigation due to the size of the modulus numbers that fit the requirements are surprisingly common, it almost always hits a viable number within the first or second loop, which is absolutely mad.

On the difficulty of the problem as a whole.

I think the main hurdle holding people back so far is people sort of vaguely know how RSA works, but that isn't going to cut it here as the solution revolves around weakening a part of the RSA algorithm itself just enough to allow data to be decrypted from an almost imperceptible leak, you will need to know the steps RSA takes and the importance of them and the security in public/private key cryptography utilizes to find what is wrong. That being the case another hurdle you will all encounter is a need for familiarity with modular arithmetic, there's a reason there are weird undescribed functions in there, you are going to need to figure out what they do and how to reverse them. It seems like a tall order, but it's all simpler than it sounds, most of you likely just don't yet know enough to see that, It will become clear how quickly and simply this little puzzle unfolds when the walkthrough is published, in the meantime, prod and poke it, you may stumble upon the answer, in theory it should be fairly obvious when viewed from the right perspective, but I suspect its one none of you are used to using when tackling security problems.

About why normal attacks don't work.

Coincidentally the fact that it weakens the algorithm is the reason regular attacks won't work, normal attacks lock in on things like weak and predictable primes, or numbers that dissolve the algorithm down to a much simpler one, these primes were chosen to be strong to prevent accidentally being able to do that, but the solution is a super simplistic version of what those attacks achieve, and as such they're overkill, you don't need to weaken the algorithm any further when you can literally extract the message with the right approach, and it was designed that way to always work, without generating any suspicious looking primes.

Sadly these clues didn't help all that much, no great revelations were achieved after this point, but they do provide some really interesting insights into the development of these sorts of problems. By day 12 it had become clear that nobody was going to solve it and I began giving clues that should effectively give the game away.

Day 12 Clue

This seems to have hit a sort of stalemate, so I have 2 clues for you today, really they shouldn't tell you more than you could figure out by looking at it, but they're also huge steps forward, firstly, this is how the ciphertexts are calculated:

\[ c_1 = \frac{(s \times r)^e}{p + s} \; mod \; n, \; c_2 = (\frac{m}{s \times r})^e \; mod \; n\]

You should be able to validate this for yourself even if some of the functions look a bit weird. Secondly RSA is actually quite simple in operation;

• take two sufficiently large and secure primes p and q
• multiply them to get n the modulus of the system
• calculate the totient, you can look into the why yourself but it should be the lowest common multiple of 1 less than p and q
• the encryption function e must be coprime to the totient and should be sufficiently large
• the decryption function d is the modular inverse of e with reference to the totient

Now you know these facts you can instead worry about how the information can be put to work for you. One final little nugget of information is to look at the public and private keys, parts of the RSA algorithm have to be kept secret for a reason, I can show you the why in the walkthrough, but secrets are secret for a good reason.

As stated above no advancement with the problem was made, but these clues did lead to an interesting line of questioning, so I'll share that as it may help people to learn something. When asked about the correct method for calculating the totient I responded with:

Taken from the wiki on RSA

Carmichael numbers are actually one of the usual RSA attacks. Some assume the lowest common multiple is the same as multiplying them, this is not true, much of the time they are the same, but not exclusively. If you did the maths you would probably find with primes they should always be the same as long as both numbers are prime, but 1 less than prime is not prime. Or at least not guaranteed to be prime, in most cases its not prime.

In fact its never had an official proof we could rely on but its well understood that every prime after 2 must be odd, otherwise it should be divisible by 2 so logically a prime minus 1 should be even and therefore cannot be prime, but thats the limitations of mathematics for you. For an example:

\[ LCM(6, 15) = 30\]

\[ 6 \times 15 \neq 30\]

You can see the problem by expressing as a product of its primes:

\[ 6 = 2 \times 3\]

\[ 15 = 3 \times 5\]

They have 3 in common, LCM only takes one giving:

\[ 2 \times 3 \times 5 = 30\]

Multiplying includes the extra 3 giving:

\[ 2 \times 3^2 \times 5 = 90\]

So there you go, as long as all prime multiples are exclusive, LCM is the same as multiply, otherwise not, in this case there's no way to guarantee it even though the chances are slim, so if you ever find an RSA algorithm that sometimes gives garbage, that might be why. Euclid's algorithm is very powerful in crypto, by the way, it's a good one to learn, it pops up everywhere. And yes you will need it to solve this one.

Which then led to a question on the difference between Euler's totient and Carmichaels totient.

Seem to be fairly interchangeable at a glance, just a different purpose. Carmichael's lambda function is the reduced totient function. It is the smallest positive divisor of Euler's totient function that satisfies the conclusion of Euler's theorem. It is used in primality testing. So its an enhancement or something, not an area of maths I know a lot about yet.

This unfortunately marks the last point where my puzzle received interaction, it seems its difficulty gradually scared everyone into believing it was insurmountable. This serves as a stark reminder of how invisible cryptographic flaws can be even when they are as plain as day, remember this next time you decide to just trust someone else's algorithm or try to write one yourself. Which means all that is left for this section is clues, so lets run through them nice and quick.

Day 14 Clue

\[ c_1 = \frac{(s \times r)^e}{p + s} \; mod \; n, \; c_2 = (\frac{m}{s \times r})^e \; mod \; n\]

One of these things is not like the others. The clue you guys have been looking for is only a couple of lines apart.

n, r, s, e = pubkey
p, q, t, d = privkey

Thats a huge honking clue, so it's all you're getting today.

Day 14 was short and sweet, but exactly like it said it practically gives away what's going on. Day 15 recognising that was not enough then proceeds to disassemble it hoping someone might spot the problem.

Day 15 Clue

Lets look at why those values are in the private key, d is obvious, its the decryption key, the others actually don't need to be there, the reason they are is purely because I wanted to indicate where they belong, they should be secret.

• t is the totient which is used to secure the cryptosystem, because of that, if it is known d can be calculated.
• p and q are the primes used to build the cryptosystem and define the totient, because of this they must also be kept secret as they can be used to generate the totient exactly the same way and if you know the totient d can be calculated and the message decrypted.

So knowing any of these will cause the cryptosystem to crumble. Of course we don't directly know any of them, but there is one potentially available to us, we need to know how to extract it, how to use that to discover the others and then how to extract the message so we can decrypt it.

At this point anyone who knows how to crack this will been screaming "Oh c'mon they've practically given the answer to you!" at the screen, I'm right there with you. Just remember, in cryptography its always obvious when you know the answer, but rarely is until you do. That said there's very little left to give away, so let's take a look at the final clue.

Day 16 Clue

Alrighty last clue today then you'll have the weekend to attack it and see if you can get to the bottom of it and today I'd like to talk about modInverse and modDivide and modular arithmetic in general.

They all seem kinda scary and confusing unknowns but they're actually stupidly simple, modular arithmetic is different to regular arithmetic because the maths we are used to can be drawn as a number line, have you ever considered what maths a clock uses? Its modular, switch 12 to 0 and you have mod 12, the number line simply bends back on itself so you get 0,1,2,3,4,5,6,7,8,9,10,11,0,1,2 see? It just cycles, which has some useful properties for encryption algorithms but they're not really that important. As for how to deal with it, mostly just ignore the "mod n" bit, it has relevance but mostly the maths is the same.

Now anyone whose ever dealt with dimensionality of mathematical systems (yes I know I'm probably talking to just me because its very weird and niche) will know altering the framework of the number line like that has consequences, one of those is that infinites now fall between 0 and n, weird, but not important and the other is commutativity and associativity may no longer work, this is important as its stuff like \(a + b\) and \(a \times b\), in this case the alteration is minor and so the result is interesting, in short, division no longer exists.

As always though mathematicians immediately come to the rescue and point out since multiplication still exists all you have to do is inverse it, but here's where it gets really weird, in modular arithmetic not every number has a multiplicative inverse let me show you in regular arithmetic. 4 has the inverse ¼, 5 has the inverse ⅕ simple right, well when numbers loop it stomps all over that and many lose their inverse because the number must be between 0 and n. Anyway knowing exactly why isn't really important but it does happen, so the first thing you do is find the modular inverse of a number under the modulus, this is what modInverse does, you can find out how to do this with Google now you know the words. modDivide takes that inverse if it exists, and multiplies by it, the same as we do with fractions, division of fractions isn't defined, so we flip it (inverse) and multiply neat huh? Again now you know what it does you can search for it.

You must rebuild these two functions to be able to undo the mathematics of the ciphertext, but now you know what they are the only thing you have left to do is figure out how to extract what you need from it and systematically dismantle the encryption scheme until you get the decryption key, from there you will be able to decrypt the message and get the flag, good luck!

That was the last clue, either you've learned enough to tackle this yourself, or you're still completely at a loss as what to do, but don't worry I'll just give you the epilogue to finish off this section then it's on to the actual walkthrough.

Epilogue

Jimmy "the leak" Johnson has slipped through the fingers of authorities once again, we know he did something but we can't prove it or bring a lawsuit to bear, nor can we track down his accomplices in the management. They will catch up with him eventually but for Madball Investments it's too late, the corruption has spoiled the core of a once great company, its workers now subject to poor remuneration terrible working conditions and unrealistic expectations with no means to report it have begun leaving in droves, with so few of its original members left and rising technical debt ACME has handed the company over to its financial teams, Madball is to be stripped of its assets and dissolved, the managerial teams no doubt including the culprit will all receive sizable bonuses this year. It is a sad day for social justice.

A little dark perhaps? But hey, 0 solves is 0 solves, bad things were bound to happen, life ain't all fairytales.

Walkthrough

Before we dive in, the absolute most important thing to remember is most new cryptographic algorithms fail, because they are flawed. This isn't because the writer intends it to be flawed but is usually due to some oversight. What's worse is usually these flaws aren't picked up on immediately because they are hard to spot, especially by the writer who is snowblind to the algorithm. This basic principle is exactly why I built this puzzle, so that more people can learn to spot these problems and prevent the release and usage of bad algorithms. The first and most important thing to remember in this hunt is that using a new algorithm is almost always a bad idea, creating them is something that needs to be done, but they need to be time-proven before they can be trusted, question anyone that does not follow this simple rule.

So first up, lets itemize what we have:

• Public key
• Ciphertext
• Key generation and encryption algorithms

At the moment the public key and ciphertext are little more than numbers so first we'll look at these algorithms.

The first thing to do is look at how its encrypted and here there are two things to notice, firstly it's very much not an \(m^e\) encryption there's a lot more going on here and every extra thing added is a potential opportunity for error not to mention adding stuff like this isn't really complicating the encryption its more obfuscating the output which is:

1. Costly to the decryption algorithm by forcing it to perform extra steps
2. Provides almost nothing in terms of security.

def encrypt(message: str, pubkey: (int, int, int, int), privkey: (int, int, int, int)) -> int:
    n, r, s, e = pubkey
    p, q, t, d = privkey
    m = bytes_to_long(message.encode('utf-8'))
    return modDivide(pow(s * r, e, n), p + s, n), pow(modDivide(m, s * r, n), e, n)

Secondly p is in the ciphertext, since it is also in the private key this is a massive red flag as it should be private.

As described earlier the output can be shown to be these equations, through use of modDivide and modInverse functions to handle the non-standard behaviour of modularity.

\[ c_1 = \frac{(s \times r)^e}{p + s} \; mod \; n, \; c_2 = (\frac{m}{s \times r})^e \; mod \; n\]

Alright now lets look at how these numbers are actually generated.

def gen_keys() -> ((int, int, int, int), (int, int, int, int)):
    p, q = getPrime(2048), getPrime(2048)
    n = p*q
    r = 0
    while math.gcd(r, n) != 1:
        r = random.randint(2, n)
    s = 0
    while math.gcd(s, n) != 1 and math.gcd(p + s, n) != 1:
        s = random.randint(2, n) * 2
    t = math.lcm(p-1, q-1)
    e = 0
    while math.gcd(e, t) != 1:
        e = random.randint((1<<16)+1, (1<<256)+1)
    d = modInverse(e, t)
    return (n, r, s, e), (p, q, t, d)

p and q are primes, no big surprise there, most cryptography uses prime factorization but right below that we can also see that \(n = p \times q\), again not unusual. It's couched in funny language for generation reasons but r, s, and e are all randomly generated, in some ways this is worse than a prime as it is sometimes possible to regenerate primes but not so random unless you know the seed and implementation which we definitely don't here. The reason why is a question of infinites, there are infinite primes, but there are 25 primes between 1 an 100, there 73 other random digits to chose from, meaning you stand more of a chance of guessing a prime than a random number. However the public key consists of (n, r, s, e) so we need not worry, we don't need to calculate them.

Interestingly r and s must be coprime to n, this will be so the modularity doesn't dissolve them, s must also be even and added to p it must still be coprime to n which is interesting even though it isn't clear why right now, e is designed to be big, not excessively big but it has some limitation on how small it can be, this is likely a defensive mechanism as small numbers are easier to break, finally there is t which is an \(LCM(p-1, q-1)\) and then used to generate d as an inverse to e. As previously discussed its quite clear this is an RSA algorithm with some additional hacks, the hacks usually suggest something dodgy going on as there's no reason not to trust RSA.

With that in mind it is obvious that p and q are our primes, n is the modulus, t is the totient, e is our encryption function and d is the decryption function, r and s are some random values that don't seem to fit into the standard and are likely just used to obfuscate what is going on. So now we know all that, looking back at our ciphertext functions, the only unknowns in there are p and m which simplifies things, e is important but known to us, its in the public key. m is our ultimate target, e is the encryption function, p is a prime and has no business being there, but its also useful. Lets rewrite c1 in terms of p:

\[ p = \frac{(s \times r)^e}{c_1} - s\]

Take a moment to confirm but you should agree this is a sufficient substitution. Obviously I've dropped the \(mod \; n\) because it doesn't matter all that much but we need to be aware it is there. Which means we know everything on the right hand side of that equation, so if I input these as such:

"crypto" is just the library where all my functions are saved. Then I can do this:

Now to do that you do have to know how to generate both modDivide and modInverse. These can be found online, you may have to manually build them yourselves a bit as I found some of the implementations are a bit off, these are mine:

def modInverse(a: int, m: int) -> int:
    g, s, t = egcd(m, a)
    if (g != 1):
        return -1
    else:
        inv = t % m
        return inv

def modDivide(a: int, b: int, m: int) -> int:
    a = a % m
    inv = modInverse(b, m)
    if(inv == -1):
        print("Division not defined")
    else:
        return (inv*a) % m

So to perform a reverse multiplication which is what divide really is in modular arithmetic, you first reduce a to its smallest form then check if it has an inverse. Then if it does have an inverse, you multiply by it, if not you can't divide, its all a little weird but trust me the maths checks out. To calculate the inverse, you need Euclid's extended algorithm, it's called egcd because the most common usage for it is calculating the greatest common divisor. It does a lot of things in modular arithmetic and thus cryptography so its a very useful tool to have at your disposal. egcd is not a standard function, some implementations are actually wrong so be careful, here is the one I use:

def egcd(a: int, b: int) -> (int, int, int):
    s,t,u,v = 0,1,1,0
    while a != 0:
        q, r = b//a, b%a
        m, n = s-u*q, t-v*q
        b,a,s,t,u,v = a,r,u,v,m,n
    gcd = b
    return gcd, s, t

All three outputs have uses for various things, gcd is self explanatory, t under certain circumstances provides an inverse , both s and t are useful in Bezout's identity. The rest of the variables are for tracking 3 layers of loops as its basically long division where you track both the result and the remainder. You can look into it in great detail as suits but trust me this does work and provides the number for p I got, which matches the number for p I generated when I created this puzzle, so in short you now have one of the primes, great, but what do you do with that?

Looking back at the ciphertext once more, we now know everything there except for m. The problem is a bunch of things we might be able to use are wrapped in a power of e our encryption function, this is quite deliberate, using it as a power makes it very difficult to undo without knowing its inverse d the decryption function. If we knew that we wouldn't need any of this and we could just extract the message like the intended recipient, we don't and so this "to the power of" trick traps us in quite a tricky conundrum. Fear not, for we now know p and this is all we need to deconstruct this algorithm from the inside out, how? Just watch.

p is more than just a prime, its one of the two primes used to define the encryption algorithm, and that's important because there's a very good reason the RSA standard tells you to keep this secret. Thanks to the way its calculated we can abuse the modulus to tell us the other prime, because \(n = p \times q\) so obviously \(q = frac{n}{p}\) meaning with a little jiggery pokery:

So now we have both primes, but what good does that do us? We can calculate the modulus, big whoop, we already know it. With both primes we can do so much more than that, we can calculate the totient:

That shouldn't be terribly groundbreaking, I've just reused the code in the original algorithm, and neither should the next bit. We know e and we know t so all we have to do is calculate the decryption function the same way they did:

We now have everything we need to decrypt our ciphertext, this is why p , q, t and d must all remain secret, the entire system falls apart if they don't. So lets go back and have one more look at the ciphertext. There's probably a whole bunch of ways you could calculate this now you know everything, but here's my way:

\[ c1 \times c2 = \frac{(s \times r)^e}{p + s} \times (\frac{m}{s \times r})^e = \frac{(s \times r)^e}{p + s} \times \frac{m^e}{(s \times r)^e} = \frac{(s \times r)^e \times m^e}{(p + s) \times (s \times r)^e} = \frac{m^e}{p + s}\]

Time for a quick course in basic algebra, multiply the two ciphertexts together, and you get \((s \times r)^e\) on both the top and bottom. Cancel those and you remove a lot of the unpleasant looking stuff. Now it's time to turn that into something workable, let's apply the decryption key.

\[ (c1 \times c2 \times (p + s))^d = (\frac{m^e}{p + s} \times (p+ s))^d = (m^e)^d = m^{e \times d} = m^1 = m\]

Multiply both sides by \(p + s\) and get just \(m^e\) which if you put it to the power of d will cancel out and provide m. Hopefully you can follow the maths there, put together in python it looks like this:

Now obviously that's still a number but that's easy to fix, notice this line in the encryption function m = bytes_to_long(message.encode('utf-8')). It's just encoded it as a long, we just have to reverse it, which looks like this:

That looks like a flag to me! The lesson to learn is NEVER leak private key particles! We can safely assume JJ deliberately built the algorithm that way so he could provide the decryption algorithm to whomever in management was paying him without needing to snatch the private key. All the obfuscation was purely to cover up what he'd done.

Only one thing remains unanswered, why was s so weirdly specified? Pretty simple actually, if you check the ciphertext, if \(p + s\) was dissolvable by n the bottom part of \(c_1\) disappears entirely, making it very tricky to undo. It had to be even as combined with a large prime which should always be odd an odd number would produce an even one which won't be prime, its a small thing but its easier to be coprime with n if the number itself is prime or at least similar to prime. That part is the smoking gun you could use to prove this was done deliberately with intent to impose the weird obfuscation, as the only reason to do that is if you're hiding something, being very hard to undo would be a benefit to the algorithm's security so it shows intent to backdoor.

Personal Notes

As a personal note a lot of the issuse people have with cryptography aside from fear is an inability to comprehend it, most people think of it like a magic black box that turns data into random noise, and though that is the ideal, it is also not possible. To understand why you have to dig a bit into maths but Shannon proved the perfect cryptosystem doesn't exist, if it did, the data would be unrecoverable, meaning it is a hash algorithm not a cryptosystem, and that would be useless.

I tend to think of cryptography more like Fourier wave analysis, you don't need to know the details of that to get this though, we have a signal, our data, that we need to transmit to some other person, we can't send it as it is because someone else might be listening and can just use their own transceiver to pick up the message/send their own. Encryption is about trying to make that signal look like random noise by overlaying a series of other waves and using constructive and destructive interference to make an entirely new wave that seems like radio static, of course we still have to retain enough of the original data that it can be reconstructed with the right analysis on the other end, but it should be distorted enough so that without the private key, it just seems like static, the key being the series of waves applied to it.

In this scenario one of the key waves used to create the series of distortions was actually used in the signal, and worse still it was isolatable due to knowledge of the others, so with a bit of work you could construct the key of interference required to extract the original signal. That's the trick really the data must exist in the final signal but neither that or the key can be extractable, of course I'm just rambling now but my point is find a way of thinking about cryptography that doesn't rely on black boxes or magic, these ideas are harmful to your development. So too with AI, yes we don't exactly know what its thinking, but to assume we know nothing is foolish, we taught it how to learn after all and can infer much about a model by how it responded to the stimuli, so calling it a black box is bad, its more like a frosted glass box, where you sort of know what is going on if you learn about how it was built.

In terms of real world applications, if you saw an algorithm like this in the real world I'm unsure if it would be better to send them to prison for their crimes or an asylum for their own safety because they clearly need help. Suffice to say this algorithm goes way beyond necessity there are plenty of flawed algorithms out there and easily available, just ask the NSA. ;)

This exercise is useful as it teaches you about encryption, RSA in general, and what sort of things you might want to look out for when making/breaking algorithms. Many times mathematicians will accidentally include something they shouldn't in an attempt to build a secure algorithm, this will help guide them to what is useful vs. what isn't and provide some quick things to look for in confirming if the algorithm is actually secure. It will also be useful when looking to crack encryption as sometimes a vulnerability in an algorithm will expose a key piece of information that may then be used in a similar way to this. Whether that be the original message, the decryption key, something that can help you calculate them, or even some weird side-channel attack that allows you to see more of the information than should be available.

Hopefully this has been insightful, good luck, and be careful out there!

Z3n!th